Symbolic methods for biochemical networks - SYMBIONT
SYMBIONT is a binational, French and German project, that develops mathematical methods and software for symbolic analysis of systems of ordinary differential equations resulting from biochemical networks. One important task of SYMBIONT is the automatic reduction of ODE models using tropical geometry methods.
Reduction of a biochemical network. A model M(n,r,p) has n species, r reactions and p parameters. In the Systems Biology Graphical Notation, molecular species are represented by rectangles and reactions by dots. Oriented edges (arrows) leave reactant species, enter reactions, and leave reactions, enter reaction products. After reduction, a network has less species, reactions and parameters.


Multiscaleness. Dynamics of multiscale systems can be represented as itinerant trajectory in a patchy phase space landscape made of slow attractive invariant manifolds. In the terminology of the singular perturbations theory slow dynamics takes place on these slow manifolds (on patches), while fast transitions (layers) occur by following the flow of the fast vector field (long arrows) away from the slow manifolds. Each slow manifold (patch) corresponds to a different reduction, therefore the reduced model changes along a trajectory.
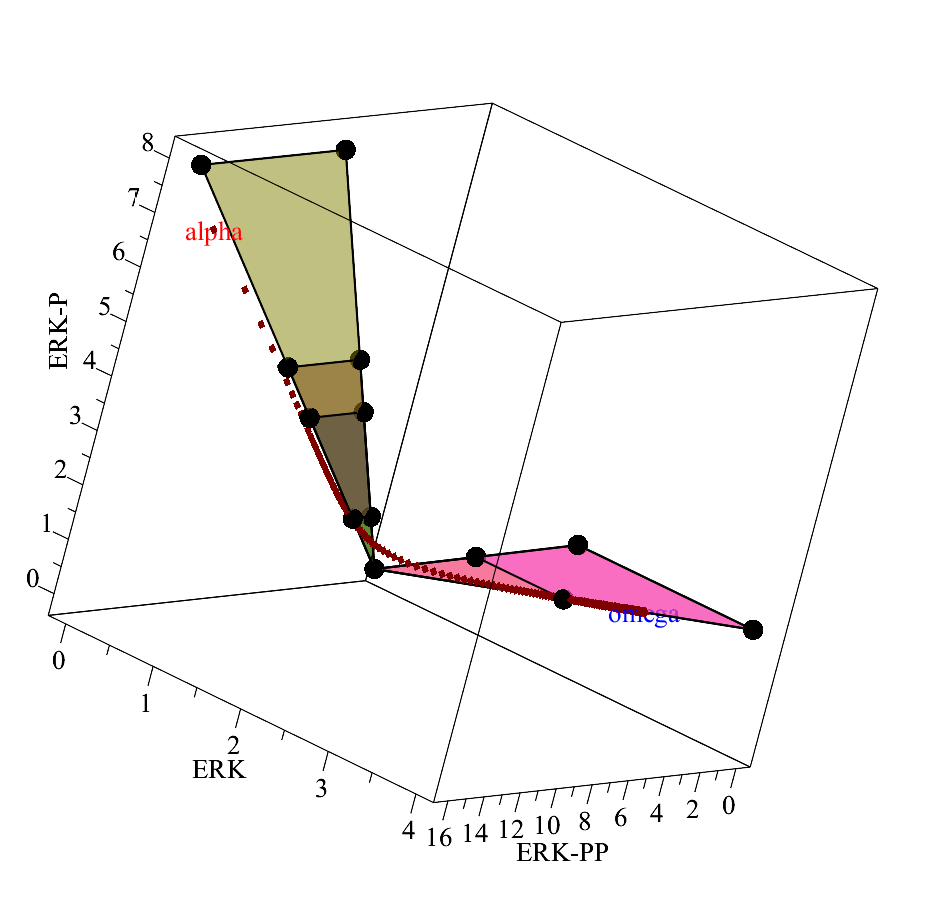
Tropical geometry methods for model reduction. Tropical geometry provides ways to compute patches of slow dynamics and the sequence of reduced models along trajectories of multiscale systems. This figure shows polyhedral tropical branches for a model of MAPK cellular signaling in projection on directions of variation of three chemical species. Each branch correspond to a region in the concentration space where a different reduced model applies. A real trajectory spans several such branches in a well defined sequence, defining the reduced models from alpha (initial condition) to omega (steady state).

We also work on automatic generation of mechanistic models of signaling pathways from phospho-proteomic data and knowledge databases. We have developed the pipeline Phos2Net allowing to extract individualized information from these databases and organize it as network models.
References
- N.Kruff, C.Lueders, O.Radulescu, T.Sturm, S.Walcher. Algorithmic Reduction of Biological Networks with Multiple Time Scales, 2020, in review Mathematics in Computer Science.
- O.Radulescu, S.Vakulenko, D.Grigoriev. Model Reduction of Biochemical Reactions Networks by Tropical Analysis Methods. Mathematical Modelling of Natural Phenomena (2015) 10: 124-138.
- O.Radulescu, A.N.Gorban, A.Zinovyev, and A.Lilienbaum, Robust simplifications of multiscale biochemical Networks. BMC Systems Biology, (2008) 2 :86.